Falhar um produto por fadiga é o terror de qualquer projeto e preocupa muito a sociedade e relato que ainda estamos aprendendo como dominá-la, já que tudo começa em escala micrométrica e na maioria das vezes não é observada no momento exato para sua correção e a quebra do produto será inevitável. Em minha jornada nesta área, relato alguns pontos importantes para tratá-la, ou seja, o mecanismo de fadiga só ocorre se tiver três eventos recíprocos, ou seja: existência de uma força de trabalho (carregamento), esforços contínuos (ciclos de carregamento) e um ponto vulnerável do componente (local para início da trinca).
A fadiga é um dano cumulativo e durante a vida de um produto, ocorrem eventos de carregamentos inesperados que causam danos contínuos, os quais se acumulam ao longo do tempo, até um ponto do aparecimento de uma trinca (nucleação) e seu aumento ocorre rapidamente até atingir um tamanho crítico, levando a uma falha abrupta em um único evento.
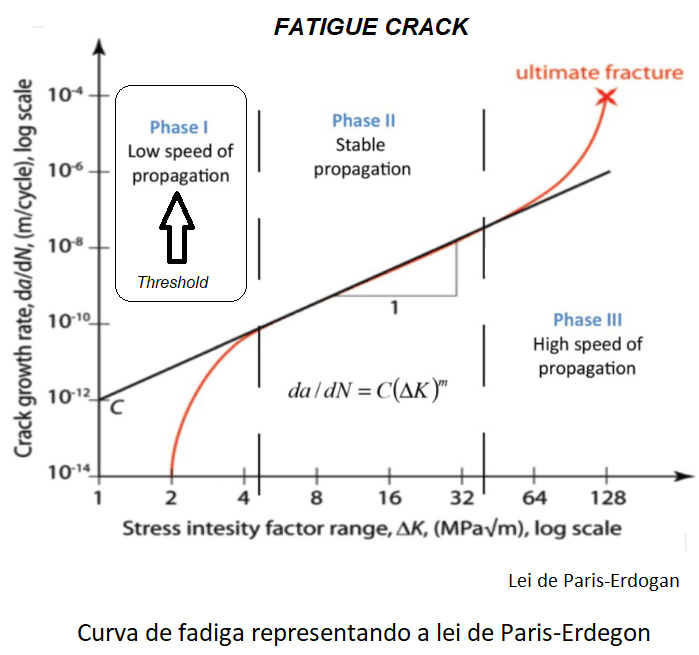A maioria dos estudos de fadiga ocorre no campo do crescimento estável da trinca, ou seja, na região II (phase II) da curva da/dN (curva da taxa de crescimento da trinca em função do fator de intensidade de tensão, conhecida como Lei de Paris-Erdogan). Cabe aqui uma observação desta técnica, ou seja, Paris-Erdogan desenvolveu uma metodologia para associar a taxa de crescimento de uma trinca com os carregamentos contínuos, levando em conta uma região em específico parametrizada geometricamente (fator de forma: Y)
Mas, para aplicarmos com eficiência estes estudos é preciso existir uma trinca para que seu crescimento seja monitorado e quantificado. Então, já que a ausência de uma trinca estável é um problema que leva a ruptura de um componente, a saída é não deixar nascer uma trinca estável; sendo um estudo de maior interesse da comunidade científica; e por isto, tecnicamente foca-se na região I da curva (phase I). Pois bem, as condições de “threshold” nesta região I são tão pequenas (< 1mm) e dependentes da microestrutura do material, que seu conhecimento remete apenas aos especialistas de materiais para entender o que realmente está acontecendo neste nível de tamanho, e um outro problema desta região é que ela não respeita uma equação da curva, ou seja, oscila muito nos valores de medição, causando mais dúvidas do que resultados positivos. Cabe aqui uma observação, um micro-defeito (inclusão, bolhas, rechupe, etc.) no material pode ser considerado similarmente a uma trinca e se comportar como tal.
Considerando que o engenheiro de projeto, com a ajuda de softers poderosos de simulação virtual, não erra ao criar um produto para uma condição de uso, de cara já eliminaremos dois critérios de preocupação: carregamento e ciclagem; portanto, resta focarmos no início da trinca.
As condições microestruturais que estão atreladas aos motivos do início da trinca é altamente dependente do processo de fabricação do componente e do processamento do material. Percebe-se a complexidade deste estudo diante de um universo de condições que estão alheias da visão da engenharia e muito dependentes de controles de qualidade das fábricas. Este tema é longo e interessante, já que o gasto de recursos nesta etapa de construção do produto compensa muito os danos que podem ocorrer no futuro, porém os mesmos estão atrelados aos melhores processos e materiais, mais critérios e controles de qualidade no produto final, todos relacionados a custos e investimentos.
Para avançar um pouco mais na discussão do mecanismo de falha mais presente em nosso meio (fadiga) é necessário voltar um pouco nos conceitos de mecanismos de falha dos materiais; então, devo esclarecer uma pergunta comum no meio. Primeiro, precisaremos entender que a propriedade limite de fadiga do componente é uma medida de força por unidade de área, ou seja, usa-se com mais frequência a unidade de medida megapascal (MPa) segundo o sistema internacional de medidas (SI). Por outro lado, qualquer produto ou material também tem sua propriedade de limite de resistência a ruptura medida em MPa. Se estamos falando de resistência a ruptura e quebra por fadiga, aparentemente ambas deveriam ter valores similares; porém, para todos os casos, o valor de limite de fadiga é bem inferior ao de resistência a ruptura; intrigante e difícil de entender como isto é possível. Percebe-se que ambas propriedades medem a resistência de um produto a falha e neste ponto surge uma pergunta “universal”: como pode o limite de fadiga de um produto ser bem abaixo do seu limite de resistência a ruptura?
A resposta anterior é esclarecida pelo conceito de “fator de intensidade de tensão”, ou seja, conceitualmente ela altera o valor do “limite de resistência a ruptura do material”; isto é, em baixos valores de carregamentos cíclicos em regime de fadiga, certas regiões pontuais podem atingir o valor do limite de resistência do material, levando-o ao aparecimento da micro trinca pontual por plasticidade, a qual passa a crescer na sequência. Percebe-se que nesta constatação aparece a definição de região pontual, isto é, “determinado ponto do produto.” A primeira alegação é que a resistência a ruptura depende da área total do produto, mas a fadiga, mesmo sendo medida por área, depende do estado geométrico de um ponto ou uma região pontual.
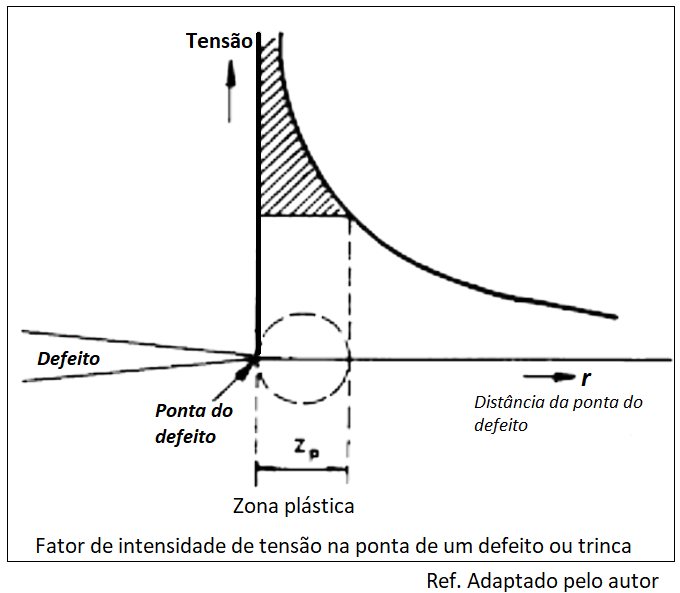A segunda alegação é referente a definição da região pontual, a qual tem um aspecto geométrico que intensifica o valor de tensão, configurado na escala macro ou micrométrica. Entalhe, canto vivo, rebarba, risco, etc. são aspectos geométricos macros; mas uma inclusão, poros, micro defeitos, grãos irregulares são aspectos micros. Engenheiros mecânicos são habituados a lidar com escalas macros, mas os de materiais conhecem bem os aspectos microestruturais da escala micrométrica.
Voltando na curva da Lei de Paris-Erdogan, a qual rege o crescimento da trinca por fadiga, observa-se três regiões distintas, a Região I, muito aplicada a conceitos da escala dimensional micro (“threshold”), Região II para a escala macro e a Região III referente ao momento do disparo da trinca. Finalizando o tema, a Região I é repleta de peculiaridades que ainda despertam o interesse de pesquisadores e estão associadas as principais falhas de produtos.
Até aqui, nota-se muita teoria de mecanismo de fadiga; mas, para discutir a sua aplicabilidade no setor automotivo, divide-se os conceitos em duas vertentes: os produtos em desenvolvimento e os em uso no campo. Para cada caso, interessa a discussão voltada para uma região da curva da Lei de Paris-Erdogan, como seguem:
Desenvolvimento de produtos: Considera-se que qualquer componente em aplicação não tem trincas na vida do veículo, por isto, a “phase II” desta curva torna-se sem interesse. Porém, a “phase I” tem uma influência pelos seus aspectos microestruturais. Os materiais apresentam micros irregularidades provenientes dos processos de fabricação em usinas ou processadores; exemplos citados anteriormente: inclusões, poros, microfissuras, dobras, etc. Os pesquisadores entenderam que os “small cracks” (>1 mm), como conhecido no meio, são causadores da redução da vida do produto e controlá-los é uma obrigação de engenharia. Percebe-se que, utilizar a curva da/dN (Lei Paris-Erdogan) não faz sentido, visto que a “phase I” não segue regras e nem equações da curva, ou seja, não se pode controlar um micro defeito pelo seu comprimento até torná-lo uma trinca estável, pelo fato de seus aspectos geométricos reduzidos não serem coerentes ao seu comportamento. A teoria bem aceita é considerar a área do defeito e aplicá-la empiricamente nos resultados das curvas tradicionais de fadiga (curvas SN, eN e curva vida) em equações empíricas. Poucos engenheiros sabem do final desta história, porque a conclusão destes conceitos foi convertida em especificações de normas de materiais, as quais quantificam valores de tamanhos, quantidades e regiões das irregularidades e garantir estes quesitos significa não ter preocupações futuras.
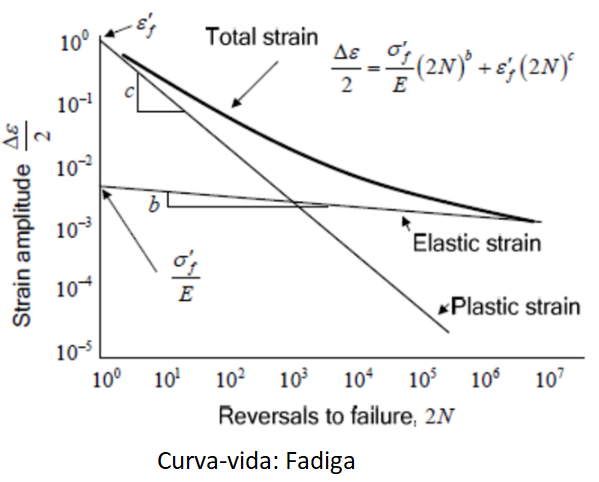Aplicação em campo ou em uso: A “phase II” da curva “da/dN x fator de intensidade de tensão” é interessante quando algum componente apresentou uma trinca em uso, partindo de um tamanho aproximado >1 mm (transição do valor de tamanho mais aceito em estudos científicos para aplicar a região II da curva, mas não mandatório). A curva da/dN consegue com precisão definir o tempo de vida deste componente pelo tamanho da trinca, cargas envolvidas, condições de uso do produto e assim, conhecer se a quebra vai ou não ocorrer. Este estudo é feito pela medição do tamanho do defeito, simulações de carregamentos e testes em laboratório com corpos de prova do material do componente em questão (teste da/dN em “CT specimens”).
Por outro lado, algumas técnicas são usadas para retardar o crescimento da trinca e prolongar ou evitar a troca do produto, seja em uma embarcação, aeronave, ferroviária, etc. Cito elas: bloqueio da trinca, preenchimento da região trincada com material de adição e alívio da ponta de trinca. No setor automotivo, na maioria das vezes, não se deseja chegar neste reparo e decide-se pela troca do componente para evitar qualquer problema posterior.
Inevitavelmente, a “phase II” da curva da/dN pode se tornar importante para casos que já ocorreram alguma falha por fadiga e o tema passa a ser um litígio; descobrir os eventos, as cargas ocorridas na vida do produto e as condições de crescimento desta trinca até a falha são fundamentais para um laudo de responsabilidade; todavia, neste momento adiciona-se outras técnicas de análise de falhas. Importante citar que, a associação das curvas de fadiga com as técnicas de microscopia eletrônica são fundamentais para associar os mecanismos de crescimento da trinca com os aspectos superficiais causados na fratura do componente, por exemplos: o crescimento da trinca de fadiga é relacionado diretamente com as estrias de fadiga, a um ponto de assumirmos que cada estria formada na superfície de fratura equivale a um ciclo de carregamento, e quantificá-las por técnicas estatísticas pode levar a um total de ciclos para a falha. Também neste campo, o avanço das análises visuais das estrias, em referência ao seu perfil e inclinação, conduz uma interpretação do estado de severidade e direção de carregamentos.
Outro ponto importante é reconhecer o tamanho da região fadigada, conhecida pelas marcas de praias superficiais e relacioná-las com o tamanho de uma trinca arbitraria corrigida pelo fator de forma de seu aspecto visual; esta quantificação é um caminho direto de correlacionar geometricamente a falha real do componente com os corpos de prova testados em laboratório durante levantamento das curvas da/dN. A maior dificuldade deste campo é achar uma equação ideal do aspecto de forma da trinca real para correção da equação do fator de intensidade de tensão e neste ponto (conhecido como o valor admissional de Y na equação), utilizam-se os “hand books” de fraturas para correlacionar estas imagens com equações de fator de forma.
Finalizando os comentários, estes estudos são interessantes e funcionam bem; porém, vale ressaltar que estas análises são extremamente complexas, visto que, normalmente observa-se um péssimo estado superficial das faces de fratura, inibindo os avanços nesta área. Os materiais não ferrosos são favorecidos neste campo pelo baixo grau de corrosividade das fraturas e maior facilidade de formação de estrias de fadiga. Alguns setores, com aeroespacial, dedicam-se muito esforços neste campo e conseguem informações ótimas de seus produtos falhados, daí um motivo para explicar longos períodos para gerar numa conclusão de uma análise de falha, por exemplo: um caso de falha de fadiga em um componente de um veículo aéreo.
